Conta-se o caso do Matemático que tentou um emprego em uma grande empresa. Quando indagado sobre o que sabia fazer, o Matemático respondeu que resolvia problemas. O Entrevistador, então, o levou a um cômodo pegando fogo. Havia uma mesa sobre a qual estava um balde com água, e o Matemático foi instruído a apagar o fogo. Ele pegou o balde, jogou a água sobre o fogo e o extinguiu. Aí, virou-se para o Entrevistador e perguntou: “O emprego é meu”? “Você terá que passar por um teste avançado”, respondeu o Entrevistador. O Matemático foi levado a outro cômodo pegando fogo. Debaixo de uma mesa, havia um balde com água e, então o Matemático foi instruído a apagar o fogo. O Matemático pegou o balde e o colocou em cima da mesa e deu por terminada a sua tarefa. O Entrevistador perguntou “Você já terminou”? O Matemático respondeu: “Sim, recorra ao problema anterior”.
Sala de Aula Virtual - Espaço destinado a discussão da Matemática e as Tecnologias da Informação.
quarta-feira, 28 de novembro de 2012
Para Relaxar: A Entrevista de Emprego de um Matemático
sexta-feira, 23 de novembro de 2012
Problemas e Soluções 28
Questão (Mantenedores): Considere T, uma aplicação linear entre os espaços vetoriais reais V e W de dimensão finita. Então podemos afirmar que:
a) Se V e W tem mesma dimensão e dimensão do núcleo de T diferente de zero, então T é injetora;
b) Se T é injetora, então dimensão de V é igual à dimensão de W;
c) Se T é injetora e sobrejetora, então dimensão de V e W são iguais;
d) Aplicando T em cada elemento de uma base V, o conjunto imagem é uma base de W;
e) Todas as afirmações são falsas.
Solução
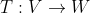 linear. Logo, dim (núcleo de T) + dim (Im T) = dim V
linear. Logo, dim (núcleo de T) + dim (Im T) = dim V
Se T é injetora, então núcleo de T = {0}
Não afirmamos, de forma geral que dim V = dim W. A resposta é c) pois dim Im T= dim W e dim núcleo de T=0.
a) Se V e W tem mesma dimensão e dimensão do núcleo de T diferente de zero, então T é injetora;
b) Se T é injetora, então dimensão de V é igual à dimensão de W;
c) Se T é injetora e sobrejetora, então dimensão de V e W são iguais;
d) Aplicando T em cada elemento de uma base V, o conjunto imagem é uma base de W;
e) Todas as afirmações são falsas.
Solução
Se T é injetora, então núcleo de T = {0}
Não afirmamos, de forma geral que dim V = dim W. A resposta é c) pois dim Im T= dim W e dim núcleo de T=0.
terça-feira, 20 de novembro de 2012
Problemas e Soluções - 27
Questão (Mantenedores): Considere as funções descritas por =x^2+x+1) e
e =xe^x-1) . Então
. Então (x)=g'(f'(x))) é:
é:
a)e^{2x})
b)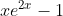
c)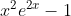
d)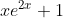
e)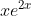
Solução
=2x+1;g'(x)=(x+1)e^x) ;
;
logo,
)=g'(2x+1)=(2x+1+1)e^{2x+1}=2e(x+1)e^{2x})
resposta a)
a)
b)
c)
d)
e)
Solução
logo,
resposta a)
sexta-feira, 16 de novembro de 2012
Problemas e Soluções - 26
Questão (Mantenedores): A equação da reta tangente ao gráfico de
=\dfrac{x^4}{4}-\dfrac{x^2}{2})
=x^3-x; f'(1)=0; f(1)=-\dfrac{1}{4})
x+b.)
no ponto de coordenada 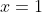 é:
é:
a) perpendicular ao eixo x;
b) passa pela origem;
c) paralela ao eixo x, com 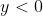 ;
;
d) da forma 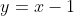
e) com equação 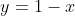 .
.
Solução
Ponto de tangencia ) ; Equação da reta
; Equação da reta  ; resposta c).
; resposta c).
Lembrete: Equação da reta tangente ao gráfico de ) em
em )) é da forma
é da forma
domingo, 11 de novembro de 2012
A utilidade da matemática
A utilidade da Matemática deve-se, em grande parte, à ampla variedade de situações que são suscetíveis de análise matemática. A seguinte história tem sido repetida várias vezes – um Matemático faz algo que parece ter apenas interesse técnico, que permanece anos sem exame (exceto talvez por outros Matemáticos) e, então, alguém encontra um uso prático totalmente inesperado. Um exemplo desta situação que afeta praticamente todos do mundo civilizado, quase todos os dias, teria surpreendido enormemente G.H. Hardy, Matemático britânico que viveu na primeira metade do século XX.
Hardy dedicou sua vida à busca pela beleza nos padrões dos números, e fez grandes contribuições à Teoria dos Números, mas via seu trabalho como Estética Matemática – guardando beleza para aqueles capazes de apreciá-la, mas não possuindo qualquer valor prático. “Nunca fiz nada de útil. Nenhuma de minhas descobertas fez e é improvável que faça, direta ou indiretamente, para o bem ou para o mal, a menor diferença para as comodidades do mundo”, ele declarou sobre suas contribuições na Teoria dos Números. Hardy não previu que, 15 anos após a sua morte, o mundo dependeria significativamente de um fenômeno que ele passou boa parte de sua carreira investigando.
Números primos são números inteiros que não tem divisores inteiros, com a exceção de 1 e do próprio número. À medida que se examinam números cada vez maiores, os primos se tornam mais infrequentes; existem 25 primos entre 1 e 100, mas apenas 16 entre 1000 e 1100, e somente 9 entre 7000 e 7100. Como estes números se tornam cada vez mais raros, fica extremamente difícil fatorar números muito grandes que são o produto de dois primos, no sentido que leva muito tempo até se encontrarem os dois primos que são os fatores. Nós confiamos nesse fato todos os dias, quando digitamos uma senha ou pegamos dinheiro em um caixa eletrônico, porque essa dificuldade de fatorar números grandes que são produtos de dois primos, é a pedra angular de muitos dos sistemas de segurança computadorizados de hoje.
Fonte: Como a Matemática explica o mundo; James D. Stein
sábado, 10 de novembro de 2012
Problemas e Soluções - 25
Questão (Mantenedores): Seja g uma função contínua nos reais e dt) . Se
. Se =-1) , então
, então ) é:
é:
a) -1 b) 1 c) -11 d) 11 e) 0
Solução: Temos=g(x)) , logo
, logo =g(1)=-1) , resposta a)
, resposta a)
Lembrete: Se g é integrável, então
=\int_{0}^{x}g(t)dt)
a) -1 b) 1 c) -11 d) 11 e) 0
Solução: Temos
Lembrete: Se g é integrável, então
é derivável e =g(x)) .
.
terça-feira, 6 de novembro de 2012
Problemas e Soluções - 24
Questão (Petrobras 2012): Seja 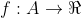 uma função dada por
uma função dada por =\sqrt{16-(x-2)^2}) , onde A é domínio tal que, qualquer outro domínio possível para f seja um subconjunto de A. Se pudermos escrever A pela notaçao [a,b], então o valor de
, onde A é domínio tal que, qualquer outro domínio possível para f seja um subconjunto de A. Se pudermos escrever A pela notaçao [a,b], então o valor de  , será:
, será:
a) -8 b) -4 c) -2 d) 6 e) 8
Solução: A é o maior domínio possível. Temos
^2=4^2-(x-2)^2=(4-(x-2))\cdot(4+(x-2))=(6-x)\cdot(2+x))
^2\geq0) , isto é,
, isto é, \cdot(2+x)\geq0) , que ocorre em [-2,6]. Assim
, que ocorre em [-2,6]. Assim =8) , cuja resposta corresponde ao item e).
, cuja resposta corresponde ao item e).
Lembrete:\cdot(h+x))
a) -8 b) -4 c) -2 d) 6 e) 8
Solução: A é o maior domínio possível. Temos
Lembrete:
quinta-feira, 1 de novembro de 2012
O Modelamento Matemático
Em Ciências, Tecnologia e outras áreas do conhecimento, quase sempre é necessário descrever ou modelar o comportamento de algum sistema ou fenômeno em estudo, em termos matemático, isto é, transformar o problema em questão em termos da linguagem matemática. Esse processo tem inicio na identificação das variáveis que se fazem presentes e que são responsáveis por mudanças no sistema, um conjunto de hipóteses compatíveis com o problema e por último, a identificação da ferramenta matemática que descreve o problema.
O modelo matemático do sistema em estudo, é muitas vezes uma equação diferencial, e esperamos que este modelo tenha uma solução que seja capaz de descrever o comportamento conhecido do sistema ou fenômeno em questão.
O modelo matemático de um sistema tecnológico ou físico, geralmente envolve a variável tempo. A solução do modelo representa o estudo do sistema, isto é, para valores apropriados do tempo t, os valores da variável dependente descrevem o sistema no passado, presente e futuro.
Como exemplo, de acordo com a lei empírica de resfriamento de Newton, a taxa de resfriamento de um corpo, é proporcional à diferença entre a temperatura do corpo e o meio ambiente. Seja t o tempo, T(t) a temperatura do corpo no instante t, e  a temperatura do meio ambiente (supomos constante durante a experiência). Se
a temperatura do meio ambiente (supomos constante durante a experiência). Se
representa a taxa de variação da temperatura do corpo em relação ao tempo, a lei de resfriamento de Newton, modela-se matematicamente como:
onde, k é a constante de proporcionalidade. Como o corpo está resfriando,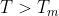 e segue-se que
e segue-se que 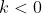 . Este modelo é uma equação diferencial ordinária linear de primeira ordem.
. Este modelo é uma equação diferencial ordinária linear de primeira ordem.
Fonte: Equações Diferenciais; Denis G. Zill e Michael R. Cullen
Fonte: Equações Diferenciais; Denis G. Zill e Michael R. Cullen
Assinar:
Comentários (Atom)