O Modelamento Matemático

          Em Ciências, Tecnologia e outras áreas do conhecimento, quase sempre é necessário descrever ou modelar o comportamento de algum sistema ou fenômeno em estudo, em termos matemático, isto é, transformar o problema em questão em termos da linguagem matemática. Esse processo tem inicio na identificação das variáveis que se fazem presentes e que são responsáveis por mudanças no sistema, um conjunto de hipóteses compatíveis com o problema e por último, a identificação da ferramenta matemática que descreve o problema.

          O modelo matemático do sistema em estudo, é muitas vezes uma equação diferencial, e esperamos que este modelo tenha uma solução que seja capaz de descrever o comportamento conhecido do sistema ou fenômeno em questão.

          O modelo matemático de um sistema tecnológico ou físico, geralmente envolve a variável tempo. A solução do modelo representa o estudo do sistema, isto é, para valores apropriados do tempo t, os valores da variável dependente descrevem o sistema no passado, presente e futuro.

          Como exemplo, de acordo com a lei empírica de resfriamento de Newton, a taxa de resfriamento de um corpo, é proporcional à diferença entre a temperatura do corpo e o meio ambiente. Seja t o tempo, T(t) a temperatura do corpo no instante t, e   a temperatura do meio ambiente (supomos constante durante a experiência). Se   

representa a taxa de variação da temperatura do corpo em relação ao tempo, a lei de resfriamento de Newton, modela-se matematicamente como:

onde, k é a constante de proporcionalidade. Como o corpo está resfriando,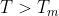 e segue-se que 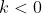. Este modelo é uma equação diferencial ordinária linear de primeira ordem.
Fonte: Equações Diferenciais; Denis G. Zill e Michael R. Cullen