Leonardo de Pisa (1180-1250) mais conhecido como Fibonacci, comerciante italiano, ajudou a popularizar o algorismo no século XIII, através de um livro clássico intitulado Liber Abaci (Livro de Ábaco), onde trata muito mais de números que de geometria. Entre os vários problemas citados, o que mais despertou a atenção dos pesquisadores foi o seguinte: Um criador de coelhos, em sua criação, depara-se com a situação- começa só com um, e cada coelho gera um coelho quando completa dois meses de idade, e a seguir gera um coelho a cada mês. Os coelhos não morrem e ignoramos os machos. Se começar com um coelho recém-nascido, após n meses, quantos coelhos terá o fazendeiro?
Para valores pequenos de n a resposta é:
Para valores pequenos de n a resposta é:
E a tabela continua. Note que para obter o número de coelhos no próximo mês, adicionamos o número de coelhos do mês anterior mais os gerados no mês corrente. Assim podemos escrever a sequência de números de coelhos em cada mês como: 1,1,2,3,5,8,13,21,55,89,144,.... Leonardo de Pisa foi sem dúvida o Matemático mais capaz do mundo cristão medieval, razão pela qual muito de sua obra era avançado em demasiado para entendimento dos contemporâneos.
Para descrever a solução do problema através de uma fórmula, colocamos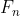 
como o número de coelhos durante o n-ésimo mês, e para n=3,4,5,... temos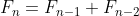 
com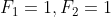 
o que é uma relação de recorrência numérica.
Citamos aqui duas identidades envolvendo os números de Fibonacci que são mais utilizadas:
A primeira é:
A segunda expressa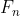 
como uma função de n, a saber:
Constata-se que a proporção entre números de Fibonacci consecutivos é aproximadamente 1,618 , isto é, para n grande a sequência de Fibonacci se comporta como uma grande progressão geométrica de razão 1,618, chamada de razão dourada.
Concluímos afirmando que a sequência de Fibonacci descreve uma vasta diversidade de fenômenos naturais, além de servir como fundamento para uma gama de algoritmos usados extensivamente em Ciências da Computação, como por exemplo, em processamento de textos, ordenação de estrutura de dados, engenharia de sofware, testes de programas.
Fonte:
1) História da Matemática; Carl Boyer
2) Fibonacci Number and computer algorithms; John Atkins; Robert Geist- West Virginia University
Nenhum comentário:
Postar um comentário