Curiosidade - 1

          Pierre Fermat (1601-1665) criou os conhecidos números de Fermat, 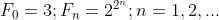   pensando que esta era uma sequencia de números primos. Para 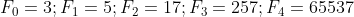, são primos.
          Em 1732, o Matemático Euler descobriu que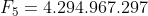    pode ser fatorado como 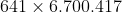, isto é,  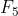é composto. A fatoração de  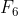foi encontrada por Laundry e Le Lasseur em 1880, a de  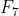em 1970 por Brent e Pollard, já a de  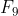em 1990 por Lenstra, Menasse e Pollard. Concluímos aqui que o problema de fatoração não é tão simples, como somos levados a pensar, pois de uma fatoração a outra há décadas de diferença. Hoje sabe-se que para  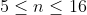não são primos.

Fonte: História da Matemática; Carl B. Boyer

Problemas e Soluções - 22

Questão (Petrobras 2012): O valor de

        

a) 0         b) -1        c) -3        d) -4        e) -5  

Solução (dois caminhos):

i)

 

ii)       e    

logo,

 cuja resposta é e).
Lembrete: Regra de L'Hospital  e  se    e   são raízes de  , então .



Problemas e Soluções - 21

Questão (Petrobras 2012): Qual é o menor valor de x que torna a expressão    verdadeira ?  Dados     e  

a)  1,625

b)  1,4558333...

c)  1

d)  0,625

e)  0,458333...

Solução :  Faça     e escreva    . Substituindo na equação, vem que   ,  cuja solução é 5 e 2. A menor é 2, assim 

 

cuja resposta é d).

Homem na Lua e a Gripe

          Às vezes ficamos impressionados com as fascinantes realizações da Ciência e da Engenharia, que temos a impressão de que todos os problemas tem solução. Durante a década de 1960, era comum escutar o seguinte comentário: Se conseguem levar o homem à Lua, como é possível que não encontrem a cura para a gripe comum?

           Hoje somos um pouco mais sofisticados do ponto de vista científico, e a maioria das pessoas está disposta a ser paciente com a Ciência em problemas desta natureza, reconhecendo que a cura da gripe comum é uma questão mais difícil do que parece à primeira vista. O sentimento geral, porém, é o de que simplesmente não encontramos a cura do resfriado comum ainda. É um problema difícil, mas levando em consideração a recompensa possível, não é de surpreender que pesquisadores da área de saúde, estejam tentando com muita dedicação, e é o que todos nós esperamos que eles encontrem a cura em algum momento. Infelizmente para aqueles que sofrem de corizas nasais e inflamações de garganta, há uma possibilidade bem real, de que uma cura para o resfriado comum jamais seja encontrada, não porque falte inteligência aos pesquisadores, mas porque a solução não existe.

Fonte: Como a Matemática explica o mundo; James D. Stein

Problemas e Soluções - 20

Questão (Petrobrás-2012): Considerando os vetores u e v unitários, tais que o produto interno , a soma u+v será um vetor:

a)  unitário;

b)  de módulo 2;

c)  nulo;

d) paralelo à u;

e) igual à diferença u-v.

Solução:   . Duas saídas:

i)
   onde  é o ângulo entre u e v. Logo,  , isto é, u e v são opostos e de mesmo módulo. Logo, u+v=0.
ii)
   

Logo,
Assim, a resposta é c).
Lembrete: O único vetor de módulo 0, é o vetor nulo.