É comum em livros de Matemática do ensino básico, o problema: Um jardim tem o formato de um retângulo. A área do jardim é de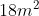 
e o comprimento excede de 3 m a largura. Quais as dimensões deste jardim?
Se c é o comprimento e L a largura, a formulação do problema de forma adimensional, é dado por: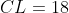 
e 
.
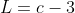Substituindo L da segunda equação na primeira, obtemos a equação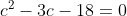 
.
Para esta equação temos duas soluções. Uma é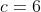 
o que leva a 
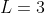, solução do problema em questão. Outra é considerar 
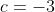, o que leva a 
, e para o problema, esta solução é descartada, pois comprimento é uma quantidade inerentemente positiva. Se esta equação ocorresse na Física, o físico não descartaria de imediato a solução aparentemente sem sentido, sem antes questionar se há algum sentido subjacente escondido nesta solução, esperando para ser revelado, como aconteceu em 1928 com Paul Dirac.
Dirac, descrevendo o comportamento de um elétron movendo-se em um campo eletromagnético arbitrário, notou que as soluções ocorriam em pares, de modo que, em certo sentido, análogo ao modo como as raízes complexas de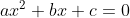 
ocorrem, na forma u+iv e u-iv. Qualquer solução em que a partícula apresentasse energia positiva, tinha uma contrapartida na qual a partícula apresentava energia negativa – uma ideia tão desnorteante quanto a um jardim com largura negativa. Dirac percebeu que isso poderia corresponder a uma partícula semelhante a um elétron, cuja carga fosse positiva (os elétrons tem carga negativa), ideia esta que foi recebida pela comunidade com ceticismo. Mas, em 1932, o físico Carl Anderson descobriu o antielétron, que foi batizado de pósitron confirmando a afirmação de Dirac. Ao restringirmos domínios, podemos estar deixando de ver algo maravilhoso e inesperado nas restrições.
Fonte: Como a Matemática explica o mundo; James D. Stein
