Curiosidade 8

Um tipo de propriedade que emerge em sistemas complexos é a organização espontânea, ou auto-organização. Um exemplo na natureza ocorre com os pássaros. Pássaros individuais, quando migrando de um lugar para outro, organizam-se inconscientemente em forma de flecha para aproveitar a aerodinâmica de seus vizinhos. Este caso são agentes individuais se organizando sem qualquer interferência de um planejador central e adquirindo propriedade coletiva, propriedade esta que nunca seria possuída pela parte individual.




Fonte: Caos e Complexidade; Ilan Gleiser

Problemas e Soluções 29

Questão (Mantenedores):  Seja        uma aplicação linear do    em 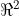. Então podemos afirmar que:
a) O núcleo de T é o espaço gerado por (1,-1,1);
b) dimensão do núcleo de T é zero;
c) dimensão da imagem de T é 1
d) {T(1,0,0); T(0,1,0); T(0,0,1)} formam uma base do ;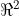
e) todas as afirmações anteriores são falsas.

Solução
   cuja solução é

. Assim, núcleo de T é gerado por (1,-1,1) com dimensão 1.
Temos : dimensão da imagem de T + dimensão do núcleo de T=3.
Se dimensão do núcleo é zero  então dim Imagem de T=3 o que é absurdo;
Se dimensão da imagem de T é 1, então dimensão do núcleo de T igual a 2, o que é falso.
Temos também, em uma base do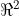 , tem 2 vetores. Assim, a resposta é a).

Lembrete: V e W espaços vetoriais de dimensão finita e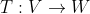  linear. Então dimensão de V=dimensão da Imagem de T+dimensão do núcleo de T.

A origem do Cálculo Diferencial e Integral

O Cálculo Diferencial e Integral é um dos pilares do desenvolvimento tecnológico, uma vez que facilita a compreensão de fenômenos naturais. É visível que uma boa parte dos estudantes em Cálculo Diferencial e Integral não dispensam a devida atenção a este disciplina, talvez por desconhecer a sua história. O Cálculo da forma como é apresentado nos dias atuais, tem a contribuição de vários cientistas em diferentes épocas, os quais passamos a relatar.

As primeiras idéias do Cálculo surgiram há aproximadamente 2500 anos, quando os gregos, entre eles Arquimedes, considerado o maior Matemático da Antiguidade, procuravam calcular área de uma figura poligonal plana fechada, dividindo-a em triângulos e somando estas áreas triangulares. Isaac Newton (1642-1716) e Wihelm Leibnitz (1646-1716) foram os criadores do Cálculo Diferencial e Integral, onde sistematizaram as idéias e os métodos surgidos em sua maioria nos Séculos XVI e XVII, com destaque para Newton que formulou o Teorema Fundamental do Cálculo. Este teorema exprime a integral em termos de outra função, fornecendo uma ferramenta simples para o Cálculo da maioria das integrais. Um passo importante para o desenvolvimento do Cálculo ocorreu com Augustin Louis Cauchy (1789-1857) que criou uma definição formal de limite, conceito que separa o Cálculo de Matemática mais elementar. Já o alemão Bernhard Riemann (1826-1866) apresentou um estudo mais aprofundado sobre integral largamente usado nos cursos de Análise Matemática, usando os conceitos de soma inferior e soma superior.

Encerrando, nos últimos 300 anos vários outros matemáticos deram importante contribuições ao Cálculo Diferencial e Integral, que encontra inúmeras aplicações nas Ciências Naturais e na Tecnologia.

Fonte: Boyer, Carl B.; História da Matemática; Edgard Blucher